Kunci Jawaban
Kunci Jawaban, Matematika Kelas 11 Halaman 23 - 24 Kurikulum Merdeka, Latihan 1.3: Komposisi Fungsi
Kunci Jawaban, Matematika Kelas 11 Halaman 23 - 24 Kurikulum Merdeka, Komposisi Fungsi dan Fungsi Invers, silakan disimak pada artikel berikut ini.
Penulis: Vanda Rosetiati | Editor: Vanda Rosetiati
TRIBUNSUMSEL.COM - Kunci Jawaban, Matematika Kelas 11 Halaman 23 - 24 Kurikulum Merdeka, Komposisi Fungsi dan Fungsi Invers, silakan disimak pada artikel berikut ini.
Kunci jawaban ini untuk buku Matematika untuk SMA/SMK Kelas XI Edisi 1 Penulis Dicky Susanto, Savitri K Sihombing dkk, Penerbit Pusat Kurikulum dan Perbukuan.
Halaman 23 dan 24 merupakan Soal Latihan 1.3, Komposisi Fungsi dan Fungsi Invers.
Selengkapnya soal dan kunci jawaban, Matematika Kelas 11 Halaman 23 - 24 Kurikulum Merdeka, Komposisi Fungsi dan Fungsi Invers.
1. Jika f(x) = √x+3 dan g(x) = x+3
a. Tentukan f(x) + g(x)
Jawaban: f(x) + g(x) = √(x + 3) + x + 3
b. Tentukan domain dan range dari f(x) + g(x)
Jawaban:
Domain:
Df : {x│x ≥ - 3, x ∈ R}
Dg : {x│x ∈ R}
Df+g = Df ∩ Dg = {x│x ≥ - 3, x ∈ R}
Range:
Rf+g = {x│x ∈ R}
2. f(x) = x^2 + 2 dan g(x) = 2x – 5
a. Tentukan f(x) - g(x)
Jawaban:
f(x) - g(x) = x^2 + 2 – (2x – 5)
= x^2 + 2 – 2x + 5
= x^2 – 2x + 7
b. Tentukan domain dan range dari f(x) – g (x)
Jawaban:
Df : {x│x ∈ R}
Dg : {x│x ∈ R}
Df-g = Df ∩ Dg = {x│x ∈ R}
Nilai minimum fungsi kuadrat y = x^2 – 2x + 7 yakni:
3. Buatlah suatu fungsi kuadrat dan fungsi eksponensial! Tentukan hasil penjumlahan dan pengurangan kedua fungsi tersebut!
Jawaban:
Contoh: 2^x + x^2 dan 2^x – x^2
4. Dua fungsi, f(x) (berwarna merah) dan g(x) (berwarna biru) diberikan di bawah ini.
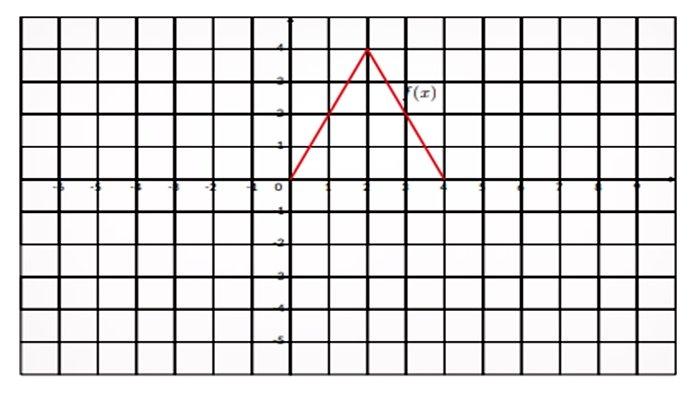
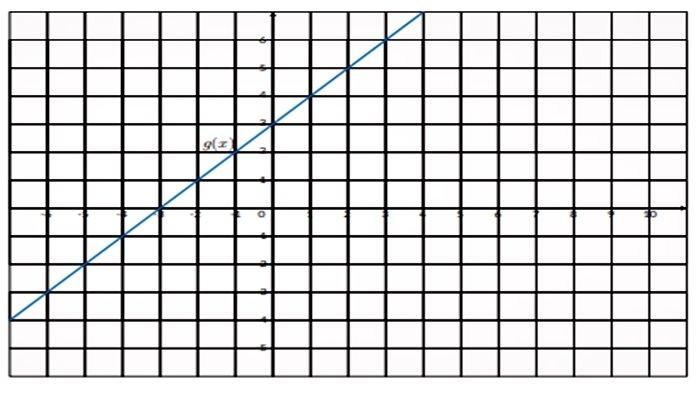
Tentukan:
a. (f + g)(2)
b. (f – g)(1)
c. (f g)(3)
d. (f/g)(4)
Jawaban:
a. 4 + 5 = 9
b. 2 − 4 = −2
c. 2 × 6 = 12
d. 0/7 = 0
5. Pendapatan dari penjualan suatu produk adalah R(x) = -20x^2 + 1000x, sedangkan biaya produksi C(x) adalah 100x + 8000.
Jumlah produk dinyatakan dalam x.
Tentukan keuntungan sebagai fungsi dari jumlah produk x.
Jawaban:
R(x) - C(x) = -20x^2 + 900x - 8000
6. Jika f(3) = 7, g(3) = 6, f(6) = 13, g(6) = 12, tentukan:
a. f(3) + g(3)
b. f(3) – g(3)
c. f(3) x g(3)
d. f(3) : g(3)
Jawaban:
a. 7 + 6 = 13
b. 7 - 6 = 1
c. 7 × 6 = 42
d. 7/6
7. Berikan contoh nyata tentang perkalian dua fungsi dalam kehidupan sehari-hari.
Jawaban:
2 kali 5 =10
Contoh penjualan mangga pembeli bilang 2 kali 5 ya om, berarti 10 mangga yang diberi kepada pembeli dan bisa digunakan saat belajar matematika.
8. Berikan contoh nyata tentang pembagian dua fungsi dalam kehidupan seharihari.
Jawaban:
Contoh nyata dari pembagian dua fungsi dalam kehidupan sehari-hari bisa ditemukan dalam perhitungan keuangan atau logistik. Misalnya:
Pembagian Biaya Restoran:
Misalkan Anda makan di restoran dengan tiga teman, dan total biaya makan adalah Rp 120.000. Jika Anda ingin membagi biaya tersebut secara merata, Anda bisa menggunakan fungsi pembagian. Dalam hal ini, fungsi pertama adalah total biaya restoran (Rp 120.000), dan fungsi kedua adalah jumlah orang yang membayar (4). Hasilnya adalah Rp 120.000 ÷ 4 = Rp 30.000 per orang.
===
*) Disclaimer:
Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.
Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.
Demikian Kunci Jawaban, Matematika Kelas 11 Halaman 23 - 24 Kurikulum Merdeka, Komposisi Fungsi dan Fungsi Invers .
Baca berita dan artikel lainnya langsung dari google news
Ikuti dan bergabung di saluran WhatsApp Tribunsumsel.com
Kunci Jawaban Siswa
Kunci Jawaban
Kunci Jawaban Matematika Kelas 11 Halaman 23 - 24
Kunci Jawaban Matematika
Kelas 11
Kurikulum Merdeka
| Jawaban Modul 3.1 Pengenalan Internet Sejak Dini, Pelatihan Internat Sehat Anak Pintar Kemenag 2025 |

|
|---|
| Kunci Jawbaan Modul 3.3 Imam dan Wawasan Kebangsaan, Pelatihan Dauroh Aimmah Pintar Kemenag 2025 |

|
|---|
| Kunci Jawaban Modul 3.1 Memahami Peran Imam Masjid, Pelatihan Dauroh Aimmah - Pintar Kemenag 2025 |

|
|---|
| Jawaban, Modul 3.7 ldentifikasi Asesmen dan Profil Peserta Didik Berkebutuhan Khusus - Bagian 2 |

|
|---|
| Jawaban: Modul 3.6 ldentifikasi Asesmen dan Profil Peserta Didik Berkebutuhan Khusus - Bagian 1 |

|
|---|










![[FULL] Citra Kabinet Prabowo Tercoreng Ulah Ebenezer, Pakar Peringatkan RI Resiko 'Angkut' Relawan](https://img.youtube.com/vi/tp44gIVjStk/mqdefault.jpg)





Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.